Parte da matemática que por objeto a resolução dos triângulos.
quinta-feira, 1 de março de 2012
Resumão...
Aqui vamos colocar um grande resumão... assim você vai saber, sobre o que este blog vai tratar.
Caso o blog não ajude muito com a trigonometria, e você queira exercícios, ou alguma explicação. talvez possamos ajudar é só mandar um e-mail para: ucsoficinasisprogacao@gmail.com
Caso o blog não ajude muito com a trigonometria, e você queira exercícios, ou alguma explicação. talvez possamos ajudar é só mandar um e-mail para: ucsoficinasisprogacao@gmail.com
quarta-feira, 29 de fevereiro de 2012
Vamos começar imaginando uma pequena história???
Numa pequena cidade de Trigonal, onde todos os projetos elaborados pela cidade eram muito bem feitos, e que não podiam ter nenhum problema. O prefeito descobriu que na praça central, havia uma rampa plana que unia dois pisos em desnível.
Então o prefeito percebeu também que subindo a rampa, a distância de 3 metros, seu deslocamento na vertical será de 1 metro.
Foi então que surgiu uma duvida. O prefeito queria saber “Qual seria o seu deslocamento na vertical se ele percorresse 6 metros na rampa?”.
Deste modo para resolver o problema do prefeito, vamos ter os triângulos OAB e OCD que são semelhantes, sendo assim teremos:
Logo, percorrendo 6 metros da rampa, seu deslocamento na vertical será 2 metros.
A razão entre o deslocamento na vertical e a distância percorrida sobre a rampa depende exclusivamente do ângulo que a rampa forma com o plano horizontal.
Podemos também relacionar o deslocamento na horizontal com a distância percorrida sobre a rampa ou ainda relacionar o deslocamento na horizontal. Essas relações também dependem do ângulo que a rampa forma com o plano horizontal.
Definiremos a seguir algumas razões entre lados de um triangulo retângulo. Essas razões são o alicerce da trigonometria.
Agora vamos ver as relações de triângulos retângulos???
Dado um ângulo agudo qualquer de medida α, considere os infinitos triângulos retângulos que possuem o ângulo de medida α. Alguns desses triângulos são:
OBS: ângulo agudo, é o ângulo que esta entre 0º e 90º.
Observe que os triângulos OAB, OCD, OEF e OGH são semelhantes. Assim, a razão entre dois lados quaisquer de um deles é igual à razão entre os lados correspondentes dos outros, ou seja:
Note que as constantes r1, r2, r3 e dependem exclusivamente da medida α, e não das dimensões do triangulo escolhido para obtê-las.
Como os infinitos triângulos que possuem o ângulo agudo de medida α são semelhantes entre si, temos que as constantesr1, r2, r3, e podem ser obtidas, de maneira análoga, a partir de qualquer um deles, ou seja:
As razões (trigonometricas) r1, r2, r3 e são chamadas respectivamente de: seno do ângulo α (sen α), cosseno do ângulo (cos α) e tangente do ângulo α (tg α).

RELAÇÃO ENTRE GRAU E RADIANOS
 Vimos que um ângulo raso determina uma semicircunferência, ou seja, 180° correspondem a π rad. Um arco de 2π rad é, portanto, um arco de volta completa, correspondendo a dois ângulos rasos, ou 360°.
Vimos que um ângulo raso determina uma semicircunferência, ou seja, 180° correspondem a π rad. Um arco de 2π rad é, portanto, um arco de volta completa, correspondendo a dois ângulos rasos, ou 360°.A tabela abaixo fornece a relação entre as medidas em grau e em radianos de alguns ângulos. Observe também a figura ao lado.
E agora vamos aprender mais sobre as Funções Trigonométricas???
INTRODUÇÃO
Considere a situação seguinte.
Ondulatória. Em certa cidade litorânea, a altura, h da maré(em metros), em função do tempo t , é dada pela função
Na qual o tempo é medido em horas, a partir da meia-noite.
Na qual o tempo é medido em horas, a partir da meia-noite.
Na expressão h(t), aparece a função trigonométrica cosseno, que descreve comportamento do tipo periódico. Além do nível das mares, outros fenômenos têm comportamento periódico, como: variação da temperatura terrestre, da pressão sanguínea e da corrente alternada, a propagação do som , etc.
DEFINIÇÃO DE FUNÇÃO PERIÓDICA
O menor valor de p que satisfaz a igualdade acima é chamado período fundamental, ou simplesmente período de f.
As funções trigonométricas seno, cosseno e tangente – tipicamente periódicas – surgem com frequência na modelagem matemática de fenômenos naturais que apresentam periodicidade, como é o caso das marés.
Assinar:
Comentários (Atom)
.jpg)
.jpg)
.jpg)
.jpg)










.jpg)
.jpg)
.jpg)
.jpg)

.jpg)



.jpg)


.jpg)


.jpg)

.jpg)

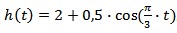












.jpg)
.jpg)